Dewar's method

Robert E. Dewar’s 1991 American Antiquity article is essentially aimed at addressing the risky assumption made by the majority of archaeological settlement distribution models that ‘components assigned to each phase or period’ are normally ‘treated as contemporaneous’ (Dewar 1991, p.604). Considering this along with the potential that standard archaeological settlement methodologies have for ‘double counting’ caused by villages moving during a phase and the same group of people being responsible for the creation of new similar-sized villages, Dewar notes quite correctly that any interpretations derived from these models are open to legitimate criticism. Dewar acknowledges that he is not the first to identify this as a potential problem (citing the ‘contemporaneity’ problems as outlined by Plog (1974) and Schacht (1984)) but he distinguishes his own model from these earlier attempts by claiming that his approach allows for single period occupations something which is less successfully afforded by the two previous attempts (Dewar 1991, p.605).

Dewar’s model assumes that the analyst has access to settlement data for the target period itself and for the periods immediately preceding and succeeding it. From these Dewar first gets the mean settlement abandonment and establishment rates for the target phase (Dewar 1991, p.608). He arrives at estimates for these rates based on the well-established Monte Carlo simulation method (Dewar 1991, p.609). He takes the abandonment rate to be equal to (a+d)/p where a equates to the amount of sites occupied during both the target and preceding phases, d is equal to the amount of sites occupied only during the target phase and finally p is the length in years of the target period. For the establishment rate he proposes (c+d)/p where both d and p are as in the previous equation and c is equal to the number of sites that were occupied both during the target and succeeding periods (see below).

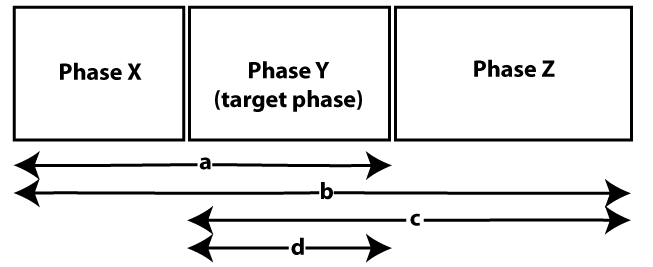
Dewar’s model begins by taking a+b for the initial amount of sites in occupation at the start of the simulation. The core algorithm basically takes the input and calculates whether it should be increased and/or decreased by 1. It does this by checking the probability of site creation and abandonment using the establishment rate and abandonment rate formulae. It then takes this output and re-enters it into the algorithm as the new input. It does this once for every p years. It then runs this process an arbitrary number of times. Dewar takes 500 as being a reasonable number of iterations (Dewar 1991, p.610). For Dewar the most interesting aspect of the iterative running of the algorithm is the standard deviation of the end results. The range of these values represents what Dewar calls the activity or ‘flux’ of settlement, a feature that he feels more accurately represents the dynamism of settlement activity, something that is noticeably absent from the traditional snapshot methods that he is critiquing (Dewar 1991, p.609).